0-1背包问题！ 回溯？？ 动态规划？？

注意：如果未特殊说明：w表示背包的容量，n表示物品的数量。

1. 什么是0-1背包问题？

对于一组不同重量、不可分割的物品，我们选择一些装入背包，在满足背包最大容量限制的前提下，背包中物品总重量的最大值是多少？

假如有n个物品，对于每个物品来说，都有两种选择，装进背包或者不装进背包。对于n个物品来说，总的装法就有2^n中装法。所以，我们只需要穷举所有的装法，去掉大于背包容量的装法，选择一个最接近背包容量的装法。

举个例子：假设背包的最大承载重量是9。我们有5个不同的物品，每个物品的重量分别是2，2，4，6，3。那我们能怎么装呢？

2. 回溯算法

我们假设函数f(x, y)，其中x为第几个物品，y为当前背包重量。可以画出如下图形。

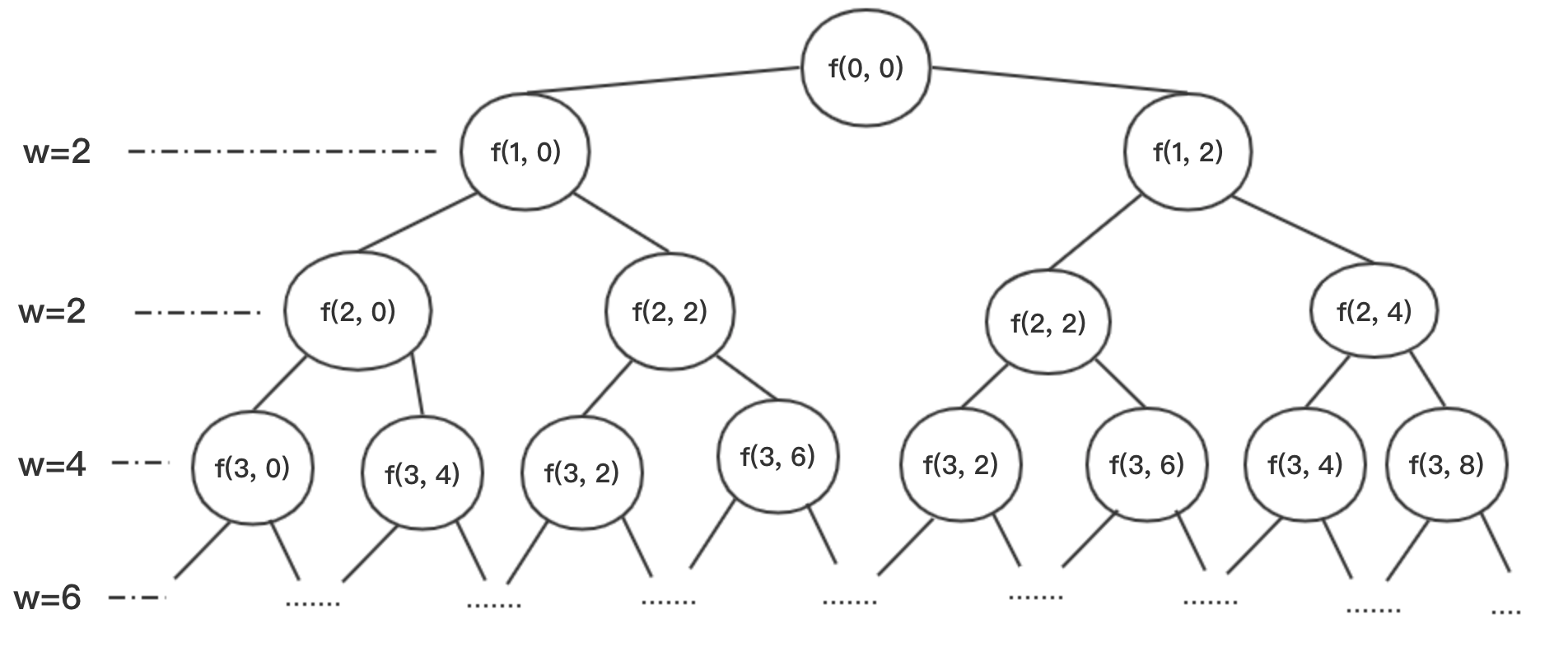
就是枚举所有的情况，得出最优解。

翻译成代码：

private int maxW = Integer.MIN_VALUE;   // 存放结果
private int n = 5;  // 物品数量
private int w = 9;  // 背包容量
private int[] weight = {2, 2, 4, 6, 3};

public function(int i, int cw) {
    if (i == n || cw == w) {    // 物品放完了，背包容量满了
        if (cw > maxW) maxw = cw;
        return;
    }
    f(i+1, cw);     // 第i+1个物品不放入背包
    if ((cw + weight[i]) <= w) {
        f(i+1, cw + weigth[i]);   // 第i+1个物品放入背包
    }
}

这就是回溯算法实现的0-1背包问题。

可以再优化吗？！！！

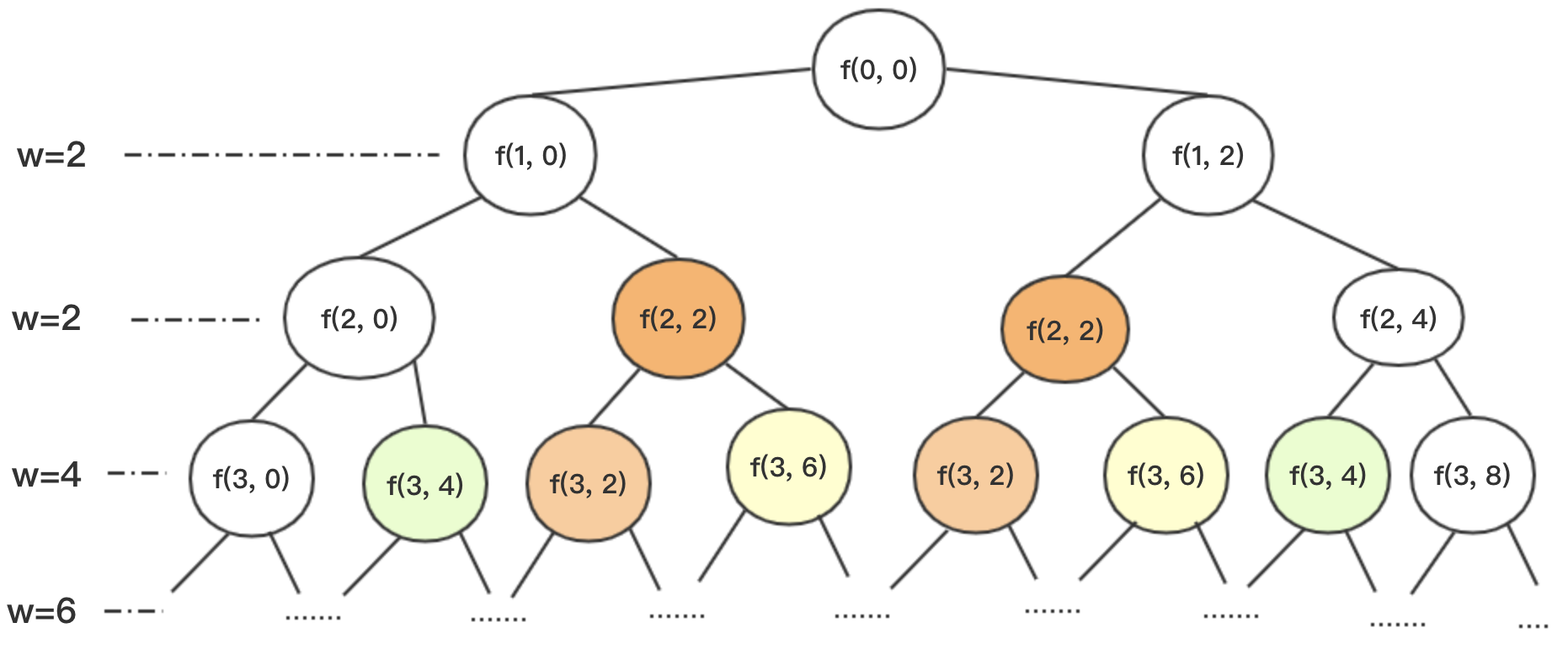
我们再看这张图，图中颜色相同的部分，求解其实是重复的，就像两个f(2,2)，下面一定都是f(3,2)和f(3,6)，所以没必要计算两次。我们只需要记录一下，我们解过哪些情况，然后记录一下，下次再进来的时候直接返回就可以啦。

private int maxW = Integer.MIN_VALUE;   // 存放结果
private int n = 5;  // 物品数量
private int w = 9;  // 背包容量
private int[] weight = {2, 2, 4, 6, 3};
private boolean[] mem = new Boolean[n][w+1];    // 加了这行

public function(int i, int cw) {
    if (i == n || cw == w) {    // 物品放完了，背包容量满了
        if (cw > maxW) maxW = cw;
        return;
    }

    if (mem[i][cw]) return;      // 加了这行
    mem[i][cw] = true;           // 加了这行
    f(i+1, cw);     // 第i+1个物品不放入背包
    if ((cw + weight[i]) <= w) {
        f(i+1, cw + weigth[i]);   // 第i+1个物品放入背包
    }
}

这种解决办法非常好。实际上，它已经跟动态规划的执行效率基本上没有差别。但是，多一种方法就多一种解决思路，我们还是要看一下动态规划是怎么解决的。

3. 动态规划

我们把整个求解过程分为n个阶段，每个阶段会决策一个物品是否放到背包中。每个物品决策（放入或者不放入背包）完之后，背包中的重量会有多种情况。例如树中第一次决策完后，背包的重量只有两种情况【0，2】，第二次决策完后，背包中只会有三种情况【0，2，4】等等。这样我们就把每一层重复的状态合并了，这样我们就能保证每一层不同状态的个数都不会超过w个（w表示背包的容量）。于是就成功避免了每层状态个数的指数级增长。

我们用二维数组states[n][w+1]，来记录每层可以达到的不同状态。
第0个（下标从0开始编号）物品的重量是2，要么装入背包，要么不装入背包，决策完之后会对应背包的两种状态，背包中的总重量是0或者2。我们用states[0][0]=true和states[0][2]=true来表示这两种状态。

依次类推，考察完所有的物品后，整个states状态数组就都计算好了。我们把整个计算过程画出来。

①初始状态

\	0	1	2	3	4	5	6	7	8	9
w=2 0	0	0	0	0	0	0	0	0	0	0
w=2 1	0	0	0	0	0	0	0	0	0	0
w=4 2	0	0	0	0	0	0	0	0	0	0
w=6 3	0	0	0	0	0	0	0	0	0	0
w=3 4	0	0	0	0	0	0	0	0	0	0

②第0个物品决策完后

\	0	1	2	3	4	5	6	7	8	9
w=2 0	1	0	1	0	0	0	0	0	0	0
w=2 1	0	0	0	0	0	0	0	0	0	0
w=4 2	0	0	0	0	0	0	0	0	0	0
w=6 3	0	0	0	0	0	0	0	0	0	0
w=3 4	0	0	0	0	0	0	0	0	0	0

③第1个物品决策完后

\	0	1	2	3	4	5	6	7	8	9
w=2 0	1	0	1	0	0	0	0	0	0	0
w=2 1	1	0	1	0	1	0	0	0	0	0
w=4 2	0	0	0	0	0	0	0	0	0	0
w=6 3	0	0	0	0	0	0	0	0	0	0
w=3 4	0	0	0	0	0	0	0	0	0	0

④第2个物品决策完后

\	0	1	2	3	4	5	6	7	8	9
w=2 0	1	0	1	0	0	0	0	0	0	0
w=2 1	1	0	1	0	1	0	0	0	0	0
w=4 2	1	0	1	0	1	0	1	0	1	0
w=6 3	0	0	0	0	0	0	0	0	0	0
w=3 4	0	0	0	0	0	0	0	0	0	0

⑤第3个物品决策完后

\	0	1	2	3	4	5	6	7	8	9
w=2 0	1	0	1	0	0	0	0	0	0	0
w=2 1	1	0	1	0	1	0	0	0	0	0
w=4 2	1	0	1	0	1	0	1	0	1	0
w=6 3	1	0	1	0	1	0	1	0	1	0
w=3 4	0	0	0	0	0	0	0	0	0	0

⑥第4个物品决策完后

\	0	1	2	3	4	5	6	7	8	9
w=2 0	1	0	1	0	0	0	0	0	0	0
w=2 1	1	0	1	0	1	0	0	0	0	0
w=4 2	1	0	1	0	1	0	1	0	1	0
w=6 3	1	0	1	0	1	0	1	0	1	0
w=3 4	1	0	1	1	1	1	1	1	1	1

因为states[4][9] == true，所以最优解就是true。

将上面的过程翻译成代码就是：

// weight:物品重量，n:物品数量，w:背包容量
public int knapsack(int[] weight, int n, int w) {
    boolean[][] states[][] = new boolean[n][w+1];
    states[0][0] = true;    // 第一行数据要特殊处理，可以利用哨兵优化
    if (weight[0] <= w) {
        states[0][weight[0]] = true;
    }
    for(int i = 1; i < n; ++i) {    // 动态规划状态转移
        for (int j = 0; j <= w; ++j) {  // 不把第i个物品放入背包
            if (states[i-1][j] == true)
                states[i][j] = states[i-1][j];
        }
        for (int j = 0; j <= w-weight[i]; ++j) { // 把第i个物品放入背包
            if (states[i-1][j] == true) 
                states[i][j+weight[i]] = true;
        }
    }

    for (int i = w; i >= 0; --i) {
        if (states[n-1][i] == true) 
            return i;
    }
    return 0;
}

实际上，这是一种用动态规划解决问题的思路。我们把问题分解成多个阶段，每个阶段对应一个决策。我们记录每一个阶段可达的状态集合（去掉重复的），然后通过当前阶段的状态集合，来推导下一个阶段的状态集合，动态的向前推进。

这个代码还可以再优化吗？！！！

public int knapsack(int[] weight, int n, int w) {
    boolean[] states[] = new boolean[w+1];
    states[0] = true;    // 第一行数据要特殊处理，可以利用哨兵优化
    if (weight[0] <= w) {
        states[weight[0]] = true;
    }
    for(int i = 1; i < n; ++i) {    // 动态规划状态转移
        for (int j = w-weight[i]; j >= 0; --j) { // 把第i个物品放入背包
            if (states[j] == true) 
                states[j+weight[i]] = true;
        }
    }

    for (int i = w; i >= 0; --i) {
        if (states[i] == true) 
            return i;
    }
    return 0;
}

这个代码相对之前的代码，将states数组从二维数组降为一维数组。空间复杂度由O(n*w)变为O(w)。

需要强调的是：代码的第8行 for (int j = w-weight[i]; j >= 0; --j)，j需要从大到小来处理。如果不按j从小到大处理的话，会出现for循环重复计算的问题。你自己画一下试试。有问题我们拿出来讨论。